These intermediate level activities look at grouping multiple characteristics of objects by using Venn diagrams and is a follow on activity from ‘Understanding Sets, Sorting and Syntax (1) designed for older children. It focuses on multiple sets that have overlapping characteristics.

Purpose

To further develop some key concepts about sets and variables that are relevant to coding, in particular, overlapping sets.

Aims

• Show that objects can be be part of more than one set at the same time
• Draw a Venn diagram to illustrate this

Equipment

• The same set of sticks and circles described in Understanding Sets, Sorting and Syntax (1)
• Large sheets of paper and markers
• (optional) Lengths of stiff cord joined into circles as an alternative to drawing the circles. (We used upholstery ‘cord’ joined with Gaffer tape)

This lesson is aimed at 9+ years. If you have not done the first lesson or if it was done in earlier years, we suggest you repeat it or at least recap on it.  You will probably want to do the activities over several lessons rather than one long one.

Multiple sets

The objects we are using have three obvious characteristics – colour, size and shape.  In the beginners activities, the pupils created or recognised single sets with 1 or more of these characteristics acting as the syntax (the ‘rules’) for sorting the objects.  The activities in this lesson use multiple sets that have overlapping characteristics. The purpose of this is show that objects can exist in multiple sets at the same time, a very important concept in computing, not just in programming but also in understanding how databases work.

For example, we have a classroom full of pupils. The pupils belong to multiple sets that we can ‘query‘.

(Check that they understand the word ‘query’ = ‘ask questions about’.  You can explain that computers use special Query languages to retrieve information from a database.  Query languages are special programmes we use to ask the computer questions about the sets of data it has stored and to ask it perform various calculations on the data before displaying the results.)

Look at some examples of multiple sets in the classroom. You could do this by asking the pupils to get into one of 6 sets.  ‘Boys’, ‘Girls’,  ‘Brown hair’, ‘Blond hair’, ‘Brown eyes’, Blue eyes.  What were the problems with this?  Obviously, if you were a boy with brown hair and blue eyes, how would you make a decision which group to join? You cannot be in three places at the same time.

You could also sort some lego and explore some possible groups – number of spots, colour etc

Let’s go back to our library example. In a library, books are sorted into sections such as fiction, non-fiction, children’s books etc. We could add different characteristics to the book to sort them into groups such as the colour of the cover or when the book was published. But there is a problem; it is not practical to arrange a library physically by grouping books that have both red coloured covers and that were produced in 2016.

However, in computing we can keep adding characteristics to the books and create groups of books without worrying about the practicalities of having to physically move a few thousand books each time or having to make decisions about which group to put a book in.

You could use a Kindle or other e-reader to illustrate the book example. Go to the bookstore and look at the way the books are grouped into different genres.  But then if you type the author’s name you get a group of all books written by that one person which may include books from different genres.  Or you can see a group of ‘best-sellers’. If you have an account, you can also look at the group of books ‘recommended’ as books you would like (based on books you have read before and which have been enjoyed by people with similar tastes to yours). This group will almost certainly include books from different genres and different authors but they will still be a ‘set’ of things with something in common i.e ‘books you might like’.

When we write programmes, we often need to tell the computer that something belongs in more than one set.  If you have already looked at databases you could revisit this and talk about some of the ways you could ‘query’ the database to retrieve information.

Venn diagrams

A Venn diagram is a visual way of showing that an object doesn’t need to be a part of just one set, it can be a part of many sets. Understanding how Venn diagrams work is an important concept in programming.  When we write code, we do not ‘draw’ Venn diagrams but we represent them in code.

.

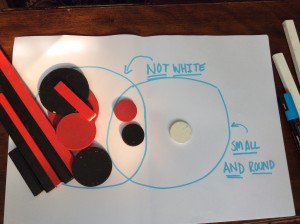
Begin with the Tell Me exercise by setting out two intersecting circles with a syntax attached to them, have pupils work out the syntax for each of the circles. So in the example above, you would start by putting all the red things in one circle and all the round things in the other circle. Then try and tease out of them how we are going to deal with an object belonging in TWO circles simultaneously. What about things which are round as well as red? Where do they go?  Then point out the intersection of the circles – this would be a good place to put them!

Try some more exercises, sticking with two characteristics. So you could have 2 sets….

• One set of big, one set of round
• One set of white, one set of small
• One set of black, one set of ‘sticks’
• One set of medium, one set of red

Vary the examples so that sometimes you create the set (Tell Me) and ask which objects go in the intersection, then move on to asking them to create the set (Show Me).

You can also challenge more able pupils by just putting some objects in the intersection and seeing if they can work backwards to working out what could be the sets in each circle.  You could also tell them that the mathematical symbol for the intersection is the upside-down U.

This is a good place to stop if you are spreading the lesson over several time slots.

AND, OR, NOT

After the pupils are familiar with the concept of an object being a part of 2 sets,  you can add in the AND, OR, NOT commands. Obviously, this complicates each of the sets and increases the difficulty. It is up to you and the ability of your class whether you want to do this.  It will definitely help them write code – and do maths – but you may want to stop here! Or you may want to do just the Tell Me exercise.  Or fast forward to the 3-circle exercise below.

So, what is at the intersection of the circles below? What are the characteristics of the sets in the circles?

It may help to split this exercise up if the pupils needs to recap on the AND, NOT,  OR functions. This can be done by building up a new group. Begin with a NOT, AND, OR command:

Then proceed to add another ring with an additional rule attached:

Following on from this exercise you could add a 3rd circle:

With two intersecting circles, you have 3 places to put an object – the 2 circles and the intersection.  If you have 3 circles which intersect you have 7 places to put an object. The additional circle increases the potential places by 4.

The classification are really no more difficult than before and the centre of the Venn Diagram (where all 3 circles overlap) is an an interesting point to cover.

From the previous 2-circle Venn diagrams,  pupils will be aware that things can be a part of more than 1 set.  Similarly, the middle intersection of the 3-circle Venn diagram shows things that are part of 3 sets.

Possible brain teasers:

• 1st Circle: NOT Black
• 2nd Circle: NOT Red
• 3rd Circle: NOT White.

• 1st Circle: Black AND Red
• 2nd Circle: Black AND Red OR White
• 3rd Circle: NOT Small

Spotting future coders! 

The first activity (just looking at 2 sets and their intersection) will help all children to understand a basic principle of coding (objects belonging in more than one set) and demonstrate computational thinking. However, there will be the occasional pupils who will be fascinated by the idea and will have no trouble in working through the AND, OR, NOT activities and the 3-circle Venn diagrams, including the brain teasers.  These may not be the most able children in your class but watch out for these kids – It is a great way of identifying the programmers of the future!